Cryptography : Intorduction, Basic Ciphers
What is Cryptograhy
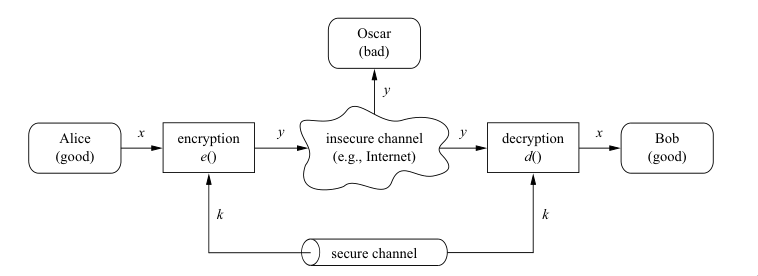
Cryptography is the science and art of securing communication and data by encoding information in a way that only authorized parties can access and understand it. Usually, the two parties that attempt to communicate are called Alice and Bob, and they communicate over an insecure channel, with an adversary Oscar attempting to understand what is being said.
Definition
Formally, a cryptographic system has the following mathematical definition:
Definition: A cryptosystem is a five-tuple $(\mathcal{P, C, K, E, D})$ where the following are satisfied:
- $\mathcal P$ is a finite set of possible plaintexts, for example, 64 bit blocks.
- $\mathcal C$ is a finite set of possible ciphertexts.
- $\mathcal K$ is the keyspace, a finite set of possible keys.
- For each key $k\in\mathcal K$, there is an encryption rule $e_k\in\mathcal E$, a decryption rule $d_k\in\mathcal D$, such that for each function pair $e_k : \mathcal P \to \mathcal C$ and $d_k : \mathcal C \to \mathcal P$, we have that \(d_k(e_k(x)) = x\) for all plaintext $x\in \mathcal P$.
Given the definition above, we can deduce that $e_k$ is an injective function. In order to then communicate over the insecure channel, Alice and Bob first secretly share their common key $k\in\mathcal K$. Bellow is a basic figure of the cryptosystem described above.
Cryptographic Security
Given the cryptographic system, we have the following classifications for the systems level of security:
- Computaionally Secure: In order to break such a cryptosystem, one would have to perform at least $N$ operations, where $N$ is some very large number. Usually refers to cryptographic systems that are computationally secure w/ respect to some crack, ie., brute force attack.
- Provable Security: In order to break such a cryptographic system, one would have to solve a NP-Complete problem (ie. prime factoring).
- Unconditionally Secure: Such a cryptographic system cannot be broken, even with infinite computational resource.
Perfect Secrecy
A cryptographic system is has perfect secrecy if Oscar cannot obtain any information from the cipertex.
Definition: A cryptographic system has perfect secrecy if the probability of $P(x | y) = P(x)$ for all plaintext ciphertext pair $x \in \mathcal P, y \in C$.
One-Time Pad (OTP)
The One-time Pad (OTP) is such a system that obtains perfect secrecy, let us first define the OTP:
Definition(OTP): Let $n\geq 1$ be the size of the information to be encoded in bits, then we know that $\mathcal P=\mathcal C = (\mathbb Z_2)^n$. And let the key space also be bits of length $n$, ie. $\mathcal K = (\mathbb Z_2)^n$. Then given a key choosen uniformly $\mathbf k\in \mathcal K$, the encryption step is defined as:
\[e_{\mathbf k}(\mathbf x) = \mathbf x \oplus \mathbf k\]And the decryption step is therefore: \(d_{\mathbf k}(\mathbf y) = \mathbf y \oplus \mathbf k\)
We know that for $n=1$, we have that $P(y=1|x=1) = \frac{P(k=0)P(x=1)}{P(x=1)} = P(k=0) = 1/2$. Similarly we can extend this argument to a theorem:
Theorem If $|\mathcal K| = |\mathcal C| = | \mathcal P |$, then the cryptosystem obtains perfect secrecy iff each key is selected with equal probability $1/|\mathcal K|$, and for each plaintext ciphertext pair $(x,y)$, there exists a unique $k\in\mathcal K$ with $e_k(x)= y$.
From this theorem we can trivially deduce that OTP has perfect secrecy.
Spurious Keys
Suppose we are in the shoes of Oscar, given a string of plaintext-ciphertex of length $n$, where the $\mathbf x = x_1x_2\ldots x_n$, and the ciphertexts are $\mathbf y=y_1y_2\ldots y_n = e_{k}(x_1)e_{k}(x_2)\ldots e_{k}(x_n)$, we know that the key produces these ciphertexts, however, it is also probible that some other keys $k^\prime$ also produces these outputs, such keys are called spurious keys.
To study the effects of spurious keys, we first define the underlying language that we are working in, ie., the probability distribution of different strings with characters in $|\mathcal P|$. For example, if we are working in the English language, the letter “q” usually is always followed by “u” (“quotient”, “quadrant”, “quiz”, vs. “qat”). To do so, we define the redundancy of the language:
Definition(Redundancy) Given $L$ is a natural language, the entropy of $L$ is defined to be:
\[H_L = \lim_{n \to \infty} \frac{H(\mathcal P^n)}{n}\]Where $\mathcal P^n$ is the n-grams of the language, with characters in $|\mathcal P|$. For example, if we define $\mathcal P$ to be the 26 english letters + 1 empty space, then $\mathcal P^3$ contains “the”, “sum”, etc. The redundancy is then defined as:
\[R_L=1-\frac{H_L}{\log_2 |\mathcal P|}\]This gives us the following theorem:
Theorem Given a cryptosystem where $|\mathcal C| = | \mathcal P|$, and keys chosen with equal probability, then the expected number of suprious keys given ciphertexts of length $n$, the expected number of spurious keys $\bar{s}_n$ satisfies
\[\bar{s}_n \geq \frac{|\mathcal K|}{|\mathcal P|^{nR_n}} - 1\]For example, if we are using a block cipher of $n$ bits, with $t$ plaintext-ciphertext pairs, then the expected number of such suprious keys are
\[2^{k-tn}-1\]Three Basic Ciphers
Shift Cipher
The shift cipher (also known as the caesar cipher) is of the oldest cipher. Such a cipher uses modular arithmetic, and the plaintext space is the set of english letters. The key is then the $26$ possible shift, ie. the key $k\in {0,1\ldots 25}$, and the encryption function is simply defined as:
\[e_k(x) = (x+k)\mod 26\]1
2
3
4
5
6
7
8
9
class ShiftCipher:
def setKey(self, k):
self.k = k
def encrypt(self, plaintext: str):
ciphertext = [(ord(c) - ord('a') + self.k)% 26 + ord('a') for c in plaintext]
return str(ciphertext)
def decrypt(self, plaintext: str):
ciphertext = [(ord(c) - ord('a') - self.k)% 26 + ord('a') for c in plaintext]
return str(ciphertext)
Affine Cipher
The affine cipher is a simple extension of the shift cipher, this time we let the key $k$ be two natual number $k=(a,b)$, where $a,b\in {0\ldots 26}$. The encryption function is defined as:
\[e_k(x) = (ax+b)\mod 26\]and the decryption function is
\[d_k(y) = a^{-1}(y-b)\mod 26\]Since $a$ might not be invertible in $\mathbb Z_{26}$ (since 26 isnt a prime), we have the additional requrement that $a$ must be invertible modulo $26$. This shrinks the key space from $26\cdot 26$ bits to $\phi(26)\cdot 26 = 12\cdot 26$ bits, where $\phi$ is the Euler-Totient function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class AffineCipher:
def setKey(self, k):
self.k = k
def encrypt(self, plaintext: str):
a, b = self.k
ciphertext = [(a * (ord(c) - ord('a')) + b)% 26 + ord('a') for c in plaintext]
return str(ciphertext)
def decrypt(self, plaintext: str):
# inverse function modulo 26
def inv(a):
for j in range(1,26):
if (j * a) % 26 == 1:
return j
a, b = self.k
a_inv = inv(a)
ciphertext = [a_inv * (ord(c) - ord('a') - b)% 26 + ord('a') for c in plaintext]
return str(ciphertext)
Substitution Cipher
Finally, we have the substitution cipher, for this cipher, the keys are the permutation (bijective) maps $\pi: \mathcal P \to \mathcal P$, and the encryption function is:
\[e_k(x) = \pi(x_1)\ldots \pi(x_n)\]1
2
3
4
5
6
7
8
9
10
class SubstitutionSipher:
def setKey(self, k):
self.k = k
def encrypt(self, plaintext: str):
pi = self.k
ciphertext = [pi(ord(c) - ord('a')) + ord('a') for c in plaintext]
return str(ciphertext)
def decrypt(self, plaintext: str):
ciphertext = [pi(ord(c) - ord('a')) + ord('a') for c in plaintext]
return str(ciphertext)